La ciencia que destaca de manera más clara las armonías de la naturaleza es, sin duda, las matemáticas. En la aritmética, exploramos un universo de figuras mediante el acto de contar; en geometría, descubrimos otro universo trazando líneas y estableciendo direcciones definidas en el campo conceptual de la imaginación; mientras que, en álgebra, producimos magnitudes de naturaleza aún más abstracta expresadas mediante letras. En todos estos casos, el primer paso consiste en establecer las condiciones generales que determinan las reglas a las que se someten todos los pasos posteriores. Cada uno de estos “universos” está impregnado de una coherencia que da lugar a una excelente simetría.
De hecho, el mundo, el universo y la naturaleza pueden ser comprendidos de manera confiable utilizando las matemáticas. En otras palabras, podríamos afirmar que la naturaleza se rige por las leyes matemáticas. Por ejemplo, la disposición de las semillas en un girasol puede entenderse mediante los números de Fibonacci. Cada número en la secuencia de Fibonacci es la suma de los dos anteriores, con la excepción de los dos primeros números. Las cabezas de los girasoles, al igual que las de otras flores, contienen dos familias de espirales entrelazadas: una que gira en sentido de las agujas del reloj y otra en sentido contrario. La forma que adopta una delicada tela de araña suspendida de puntos fijos, o la sección transversal de las velas que ondean al viento, es una catenaria, una curva simple definida por una fórmula sencilla. Las conchas marinas, los cuernos de los animales y la cóclea del oído son espirales logarítmicas que pueden generarse mediante una constante matemática conocida como la proporción áurea. Las montañas y los patrones de ramificación de los vasos sanguíneos y las plantas son fractales, una clase de formas que exhiben estructuras similares a diferentes aumentos. La famosa ecuación de Einstein, E = mc2, define la relación fundamental entre la energía, la materia y la velocidad de la luz. Además, algunas constantes simples, como la constante gravitatoria, la constante de Planck y la velocidad de la luz, son ejemplos fundamentales para comprender mejor nuestro universo en su conjunto.
Los cuadrados mágicos destacan como ejemplos notables de la armonía intrínseca de los números, algunos incluso los consideran como intérpretes del orden cósmico que rige toda la existencia. ¿Pueden realmente desempeñar ese papel? Tal vez. Aunque puedan considerarse simplemente juegos intelectuales, no solo ilustran la naturaleza de las matemáticas, sino que también, de manera incidental, reflejan la naturaleza de la realidad gobernada por la regularidad matemática. Este aspecto es incidental porque el descubrimiento de los cuadrados mágicos tiene una historia extraordinaria.
Los cuadrados mágicos son cuadrículas con una disposición única de números en su interior. Estos números son excepcionales porque cada fila, columna y diagonal suma el mismo número. Se comprenden como un todo cuadrado, cuya suma es constante en filas, columnas y diagonales. Los cuadrados mágicos, parecidos a preguntas de Sudoku, pueden variar en los números que se colocan en el cuadrado según su tamaño. Por ejemplo, tomemos un cuadrado de 3×3 y planteemos la pregunta: ¿cómo se pueden colocar los números del 1 al 9 de manera que todas las sumas de filas, columnas y diagonales sean siempre iguales? Os sugiero que os toméis un momento para reflexionar sobre esta pregunta. Descubriréis que no es tan fácil como parece. La respuesta se encuentra en la Figura 1.
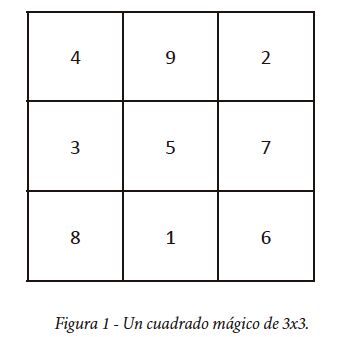
La historia del desarrollo de los cuadrados mágicos también es fascinante. El registro más antiguo de cuadrados mágicos proviene de China, aproximadamente del año 2200 a.C., y se llama Lo-Shu. Cuenta la historia de cómo el emperador chino Yu descubrió accidentalmente el primer cuadrado mágico hace 4.200 años mientras paseaba por el río Amarillo (río Lo). El caparazón de una tortuga que encontró tenía forma de cuadrado mágico, y este cuadrado dividido en cuadrículas contenía puntos en lugar de números. Podéis imaginar tener la misma cantidad de puntos en lugar de números (ver Figura 2).

Según la leyenda, el emperador Yu tomó a la tortuga y la cuidó como a una valiosa invitada en su palacio. Su fama se extendió por todo el mundo y trasciende el tiempo hasta la actualidad. Podría merecer el título de la tortuga matemática más famosa del mundo, dejando una huella sobresaliente en la historia. Después de la historia de la tortuga, los cuadrados mágicos se han convertido en un símbolo místico muy significativo en China, especialmente en la filosofía del Karma.
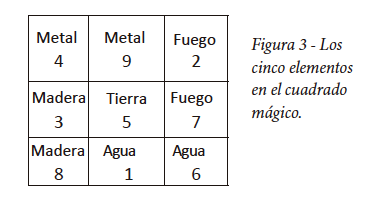
En la filosofía del Karma, se dice que el mundo está rodeado por cuatro elementos esenciales, y esto se simboliza con cuadrados mágicos. Considerando el número 5 en el centro como el mundo, los seguidores de esta filosofía rodearon el mundo con números que representaban los cuatro elementos del Yin Yang. El 4 y el 9 simbolizan el metal, el 2 y el 7 el fuego, el 1 y el 6 el agua, y el 3 y el 8 la madera, como se muestra en la Figura 3.
Los cuadrados mágicos no solo tienen significados místicos en China, sino también en muchos otros lugares. Por ejemplo, en la Arabia preislámica, la gente colgaba cuadrados mágicos en sus casas como amuletos que, según creían, protegían sus hogares de los malos espíritus. Una explicación a esta superstición podría ser que los astrólogos árabes utilizaban cuadrados mágicos para emitir horóscopos.
Los cuadrados mágicos fueron introducidos en el mundo occidental a través de la obra de Teón de Esmirna, siendo su obra más importante Expositio rerum mathematicarum ad legendum Platonem utilium. Este manual destinado a estudiantes de filosofía demuestra la interrelación entre números primos, números geométricos como los cuadrados, progresiones, música y astronomía. Su título, bastante curioso, significa que estaba destinado como introducción al estudio de las obras de Platón, lo que suena bastante fantasioso. En la sección dedicada a los números, Teón adopta un enfoque pitagórico, explorando diversos tipos de números como impares, pares, primos, compuestos, cuadrados, oblongos, triangulares, poligonales, circulares, esféricos, números sólidos con tres factores, piramidales, perfectos, deficientes y abundantes. La difusión del conocimiento sobre cuadrados mágicos en el mundo occidental también se vio impulsada por los trabajos del matemático griego Moschopoulos en el año 1300 d.C. Hoy, más de 700 años después, los cuadrados mágicos siguen siendo utilizados por profesores en el aula como herramientas para resolver problemas y practicar la suma.
En el siglo XVI, Cornelius Agrippa (1486-1535), médico, astrólogo y teólogo católico, construyó cuadrados mágicos de órdenes 3, 4, 5, 6, 7, 8 y 9, asociándolos con los siete planetas astrológicos conocidos: Saturno, Júpiter, Marte, el Sol, Venus, Mercurio y la Luna (en esa época, el Sol y la Luna se consideraban planetas). La vida de Agrippa fue pintoresca, incluyendo varios enfrentamientos peligrosos con la Iglesia, y desempeñó roles diversos como erudito ocultista, abogado y estratega militar. La obra de Agrippa, De Occulta Philosophia, estimuló el estudio renacentista de la magia e introdujo su nombre en las primeras leyendas de Fausto. Agrippa sostenía la creencia de que un cuadrado mágico que contenía la cifra 1, exhibiendo la constante mágica de 1 en todas las direcciones, representaba la perfección eterna de Dios.
En la India, la relación con los cuadrados mágicos va más allá de la mera consideración matemática, extendiéndose a la vida cotidiana, las creencias y las tradiciones. Los cuadrados mágicos, conocidos como las inscripciones Jaina, ocuparon un lugar destacado en la producción de estos objetos matemáticos. El primer cuadrado de 4×4 se descubrió en una puerta en Khajuraho, India, alrededor del año 1100 d.C. (Figura 4). El jainismo, una filosofía india establecida en el siglo VI a.C., puede haber influido en la importancia dada a los cuadrados mágicos en esta tradición.

En la India, estos cuadrados se han integrado en la vida cotidiana y se utilizan en prácticas supersticiosas. Por ejemplo, una creencia aún practicada hoy en día consiste en escribir un cuadrado mágico de 3×3 para encontrar a alguien desaparecido y colgarlo como un aviso. Curiosamente, el aviso no incluye el nombre de la persona desaparecida. Además, se cree que una pareja puede salvar su matrimonio si consigue una copia de un cuadrado mágico dibujado en un miércoles o un viernes.
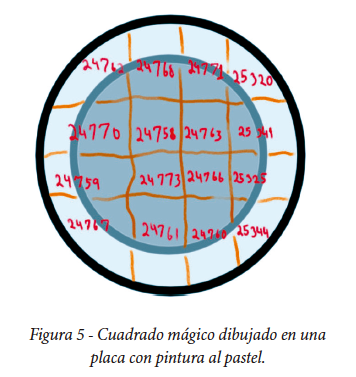
Para los matemáticos, tiene sentido que las sumas de los cuadrados de cada fila, columna o diagonal sean iguales. Sin embargo, las expectativas de los cuadrados son diferentes en la cultura india. Un ejemplo es el cuadrado que las jóvenes utilizan para buscar pareja, como se muestra en la Figura 5. Este cuadrado se pinta en un plato con pasteles, y el plato se lava en el río Ganges. La joven que busca a su futuro esposo bebe el agua coloreada con los pasteles del río. Esta tradición sigue practicándose en la actualidad.
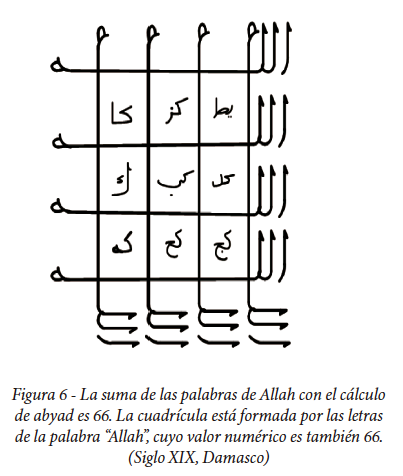
En el periodo islámico, los musulmanes también utilizaron cuadrados, y uno de los ejemplos más hermosos es el cuadrado diseñado para expresar el nombre de Dios, como se muestra en la Figura 6. Este cuadrado, con 66 letras en cada lado, evoca la suma de la palabra árabe “Allah” en el cálculo Abyad, donde a cada letra se le asigna un valor numérico.
A lo largo de la historia, la humanidad ha sentido una profunda influencia de las matemáticas y los números, y ha buscado desvelar los misterios inherentes a ellos. La prolongada fascinación de la humanidad por las matemáticas surge del reconocimiento de que el universo está construido sobre un tejido matemático. En 1623, Galileo Galilei fortaleció esta creencia al afirmar su credo: “El gran libro de la naturaleza está escrito en símbolos matemáticos”. La doctrina de Platón sostenía que Dios es un geómetra, mientras que Sir James Jeans creía que Dios experimentaba con la aritmética. Newton, por su parte, suponía que Dios puso inicialmente a los planetas en órbita, pero incluso después de que Dios decretara la ley de la gravitación, los planetas requerían ajustes continuos en sus órbitas. De manera similar, los cuadrados mágicos han representado una de esas dimensiones misteriosas de las matemáticas que han influido en la vida humana de diversas maneras.


